1月号（道順を考える問題）

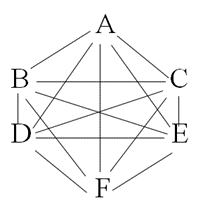
下の図のように、A～Fの６つのアルファベットが、それぞれ線で結ばれています。
アルファベットを一つ選んでから一度通ったアルファベットを通らないように、６つ全てを通る道順は何通りありますか。

【問題制作：菅野智仁】

応募方法：はがき、FAX、メールのいずれかでお送りください。

正解は3月号に掲載します。

記載内容：郵便番号、住所、氏名（匿名可）、年齢、解答（できたら計算方法なども）

締切日：1月31日（土）必着

宛先：339-0053　岩槻区城町 2-11-48　ひなまちデザイン

ら・みやび：奥山吉寛

℡：（携帯）090-3919-9406 / 048-758-0911

fax：048-878-8322

ﾒｰﾙ：tamezou@kyf.biglobe.ne.jp

---

◆１１月の解説

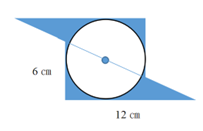
　色の塗られた部分の面積を求める問題でした。求積するには、円の半径の情報が不足しているため、まずは半径（ｒ）を計算で求めます。

　まず、図のように補助線を引くと、下半分の直角三角形を、円の中心を一つの頂点とした二つの三角形に分けることができます。このことから、以下の等式が成り立ちます。

（６×ｒ÷２）＋（１２×ｒ÷２）＝１２×６÷２
ｒ＝４

　　　　　　　　　　　　　　　

この情報を用いて、二つの直角三角形（合わせて長方形）から半径４ｃｍの円の面積を引いて求積します。

（６×１２）－（４×４×π）＝－１６π＋７２

よって答えは 「－１６π＋７２㎠」 になります。

－正解者－（敬称略）

おたかさん、坂主明子、穴澤義章、たかせき、安齋久則、八十翁、ちっち、MITSU!、109ウッサン、Tiny Uncle、たらいぶね、紫七部、winteraespa、サトシナカモト、うさぎろん、すうトレ

努力なし！70歳から脳が成長するすごいライフスタイル [ 加藤俊徳 ] 価格:1540円 (2026/1/14 22:54時点) 感想(2件)